Analyzing global internet patterns

Analyzing global internet patterns#

A DataCamp challenge      Jan, 2025

k-means clustering

Executive Summary#

This analysis categorizes countries into three distinct groups based on the rate and pattern of internet adoption between 2000 and 2022:

  1. Early Adopters: Countries in this group experienced rapid internet usage growth, particularly in the early years, surpassing 60% by 2007 and exceeding 90% by 2022. The steep initial growth reflects early investment in internet infrastructure, followed by a plateau in recent years, indicating market saturation.

  2. Mid Adopters: These countries showed a more gradual adoption curve, reaching 40% internet usage by 2012 and steadily growing. By 2022, nearly 80% of the population was online. However, a visible slowdown suggests they may not reach the adoption levels of early adopters, potentially plateauing below 90%.

  3. Late Adopters: These countries saw much slower internet growth initially, but adoption accelerated after 2010. By 2022, internet usage reached approximately 40%, indicating continued growth. However, a recent tendency toward flattening at this lower adoption rate (~40%) suggests the curve may plateau prematurely.

In conclusion, early adopters are approaching full internet penetration, while mid and late adopters are showing signs of slower growth before reaching higher usage levels. Continued investment in infrastructure may be necessary to support further growth, particularly for late adopters.

The project#

The dataset highlights internet usage for different countries from 2000 to 2023. The goal is import, clean, analyze and visualize the data to understand how internet usage has changed over time and the countries still widely impacted by lack of internet availability.

The data#

Column name

Description

Country Name

Name of the country

Country Code

Countries 3 character country code

2000

Contains the % of population of individuals using the internet in 2000

2001

Contains the % of population of individuals using the internet in 2001

2002

Contains the % of population of individuals using the internet in 2002

2003

Contains the % of population of individuals using the internet in 2003

….

…

2023

Contains the % of population of individuals using the internet in 2023

Data validation#

Hide code cell source 
# Import packages
import geopandas as gpd
import matplotlib.pyplot as plt
import missingno as msno
import numpy as np
import pandas as pd
import plotly.express as px
import plotly.graph_objects as go
import seaborn as sns
from sklearn.cluster import KMeans

# Read the data
df = pd.read_csv("data/internet_usage.csv")
df
Country Name Country Code 2000 2001 2002 2003 2004 2005 2006 2007 ... 2014 2015 2016 2017 2018 2019 2020 2021 2022 2023
0 Afghanistan AFG .. 0.00472257 0.0045614 0.0878913 0.105809 1.22415 2.10712 1.9 ... 7 8.26 11 13.5 16.8 17.6 18.4 .. .. ..
1 Albania ALB 0.114097 0.325798 0.390081 0.9719 2.42039 6.04389 9.60999 15.0361 ... 54.3 56.9 59.6 62.4 65.4 68.5504 72.2377 79.3237 82.6137 83.1356
2 Algeria DZA 0.491706 0.646114 1.59164 2.19536 4.63448 5.84394 7.37598 9.45119 ... 29.5 38.2 42.9455 47.6911 49.0385 58.9776 60.6534 66.2356 71.2432 ..
3 American Samoa ASM .. .. .. .. .. .. .. .. ... .. .. .. .. .. .. .. .. .. ..
4 Andorra AND 10.5388 .. 11.2605 13.5464 26.838 37.6058 48.9368 70.87 ... 86.1 87.9 89.7 91.5675 .. 90.7187 93.2056 93.8975 94.4855 ..
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
212 Virgin Islands (U.S.) VIR 13.8151 18.3758 27.4944 27.4291 27.377 27.3443 27.3326 27.3393 ... 50.07 54.8391 59.6083 64.3775 .. .. .. .. .. ..
213 West Bank and Gaza PSE 1.11131 1.83685 3.10009 4.13062 4.4009 16.005 18.41 21.176 ... 53.6652 56.7 59.9 63.3 64.4 70.6226 76.01 81.83 88.6469 86.6377
214 Yemen, Rep. YEM 0.0825004 0.0908025 0.518796 0.604734 0.881223 1.0486 1.24782 5.01 ... 22.55 24.0854 24.5792 26.7184 .. .. 13.8152 14.8881 17.6948 ..
215 Zambia ZMB 0.191072 0.23313 0.477751 0.980483 1.1 1.3 1.6 1.9 ... 6.5 8.8 10.3 12.2 14.3 18.7 24.4992 26.9505 31.2342 ..
216 Zimbabwe ZWE 0.401434 0.799846 1.1 1.8 2.1 2.4 2.4 3 ... 16.3647 22.7428 23.12 24.4 25 26.5883 29.2986 32.4616 32.5615 ..

217 rows × 26 columns

Missing data is marked as “..”. I will replace “..” with NaN values to map out blank cells with the help of missingno library.

Hide code cell source 
# Replace ".." with missing values
df = df.replace({"..": np.nan})

# Plot missing values map
msno.matrix(df)
plt.show()
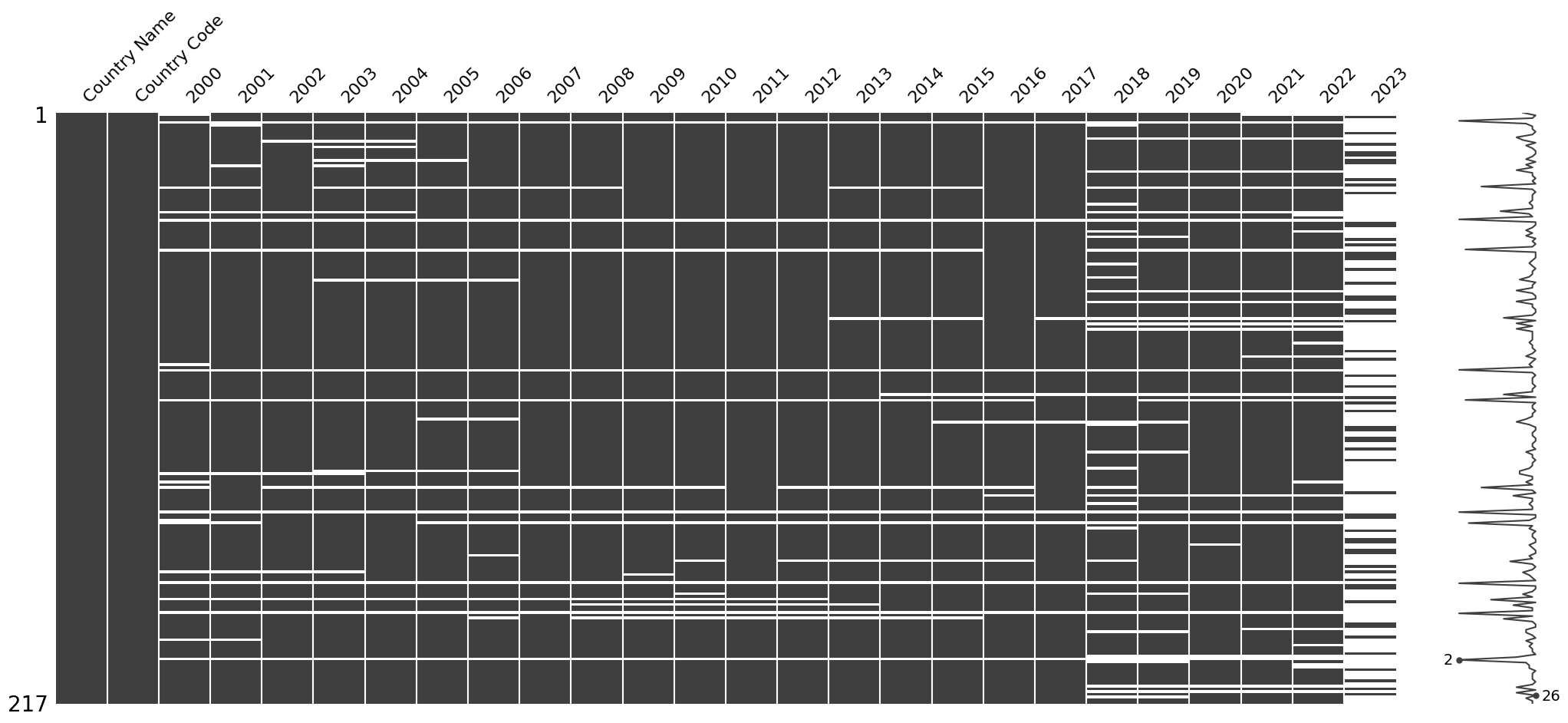
../_images/8588940a072a5b8d271596fdef5463a3e044114b5dbf1c734fa98357083d02bd.png

The data from many countries is missing for the last recorded year, 2023. Even if I interpolate it using data from the previous year, the trends will flatten, and this may distort the reading of reality, so I will drop 2023 column.

Hide code cell source 
# Drop 2023 year
df = df.drop("2023", axis=1)

Convert numerical columns to float.

Hide code cell source 
# Convert to float type numerical columns only
df[df.columns[2:]] = df[df.columns[2:]].astype("float")

Check duplicates:

Hide code cell source 
# Check on all columns
print(f"Duplicated rows in whole table -> {df.duplicated().sum()}")

# Check on numeric columns
print(
    f"Duplicated rows in the numeric table -> {df.duplicated(subset=df.columns[2:]).sum()}\n"
)

# Show duplicated
df.loc[df.duplicated(subset=df.columns[2:]), :]

Duplicated rows in whole table -> 0
Duplicated rows in the numeric table -> 6
Country Name Country Code 2000 2001 2002 2003 2004 2005 2006 2007 ... 2013 2014 2015 2016 2017 2018 2019 2020 2021 2022
39 Channel Islands CHI NaN NaN NaN NaN NaN NaN NaN NaN ... NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
94 Isle of Man IMN NaN NaN NaN NaN NaN NaN NaN NaN ... NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
146 Northern Mariana Islands MNP NaN NaN NaN NaN NaN NaN NaN NaN ... NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
172 Sint Maarten (Dutch part) SXM NaN NaN NaN NaN NaN NaN NaN NaN ... NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
183 St. Martin (French part) MAF NaN NaN NaN NaN NaN NaN NaN NaN ... NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
200 Turks and Caicos Islands TCA NaN NaN NaN NaN NaN NaN NaN NaN ... NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN

6 rows × 25 columns

Duplicates correspond to numeric columns in countries with no data at all. I will drop these rows.

Hide code cell source 
# Drop rows with no values at all
df = df.drop_duplicates(subset=df.columns[2:])

To further eliminate missing values I will linearly interpolate the gaps across columns (years).

In the case of consecutive NaNs, I will fill them both forward and backward, with a limited number of consecutive NaNs. But how do we determine the maximum number of consecutive NaNs to fill? Let’s analyze how many countries with remaining NaNs are removed based on the limit we choose.

Hide code cell source 
# Init lists
n_countries_with_nan = []
n_limit = []

# Iterate through a limit range
for limit in range(1, 10):
    # Interpolate
    interpolated = df.loc[:, df.columns[2:]].interpolate(
        limit=limit, limit_direction="both", axis=1
    )

    # Build dataframe with interpolated values
    dfi = df.loc[:, ["Country Name", "Country Code"]].join(interpolated)

    # Get number of missing values per row
    nans = dfi.isna().sum(axis=1)

    # Show countries with still missing values
    df_nans = dfi.join(nans.to_frame(name="nans"))
    df_nans = df_nans.loc[df_nans["nans"] != 0, ["Country Name", "nans"]]

    # Store the number of countries still with missing values
    n_countries_with_nan.append(len(df_nans))
    n_limit.append(limit)

# Plot
limit_df = pd.DataFrame(
    {"n_limit": n_limit, "n_countries_with_nan": n_countries_with_nan}
)
fig, ax = plt.subplots(figsize=(4, 3))
sns.pointplot(x="n_limit", y="n_countries_with_nan", data=limit_df, ax=ax)
ax.set_xlabel("Year-limit of consecutive NaN filling", size=10)
ax.set_ylabel("Number of countries still with NaNs", size=10)
sns.despine()
plt.show()
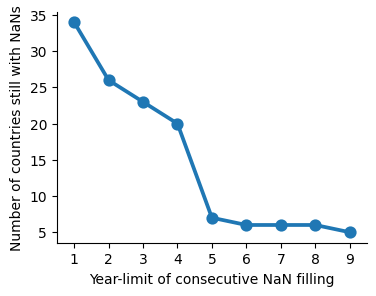
../_images/f31007737f37659aa7f2bea6dc6956886de79faad57458dc6924bc383a3fa960.png

By limiting the filling of missing values to 5 consecutive years, we significantly reduce the number of countries that still have gaps. Assuming that values can be carried over for these 5 years may be a big assumption, but since I want to include the maximum number of countries in the study, I will use this as the cutoff criterion.

Hide code cell source 
# Define limit years to fill NaNs
limit = 5

# Interpolate
interpolated = df.loc[:, df.columns[2:]].interpolate(
    limit=limit, limit_direction="both", axis=1
)

# Build dataframe with interpolated values
dfi = df.loc[:, ["Country Name", "Country Code"]].join(interpolated)

# Get number of missing values per row
nans = dfi.isna().sum(axis=1)

# Show countries with still missing values
df_nans = dfi.join(nans.to_frame(name="nans"))
df_nans = df_nans.loc[df_nans["nans"] != 0, ["Country Name", "nans"]]
df_nans
Country Name nans
3 American Samoa 23
50 Curacao 11
75 Gibraltar 1
103 Korea, Dem. People's Rep. 4
105 Kosovo 12
150 Palau 13
178 South Sudan 8

These are the countries that still have NaNs. Given their population relevance, I will take a closer look at South Sudan and North Korea to understand what’s going on with them.

Hide code cell source 
# Show South Sudan
dfi.loc[dfi["Country Name"] == "South Sudan", :]
Country Name Country Code 2000 2001 2002 2003 2004 2005 2006 2007 ... 2013 2014 2015 2016 2017 2018 2019 2020 2021 2022
178 South Sudan SSD NaN NaN NaN NaN NaN NaN NaN NaN ... 2.2 2.6 3.0 3.5 4.1 4.8 6.7 9.27123 9.64241 12.1407

1 rows × 25 columns

South Sudan has no initial records because it was only recently declared an independent country, which explains the NaNs. Since the existing values are very low, I will fill in the NaNs with 0 to include this country in the analysis.

Hide code cell source 
# Fill NaN with 0 for South Sudan
dfi.loc[dfi["Country Name"] == "South Sudan", :] = dfi.loc[
    dfi["Country Name"] == "South Sudan", :
].fillna(0)

# Show North Korea
dfi.loc[dfi["Country Name"] == "Korea, Dem. People's Rep.", :]
Country Name Country Code 2000 2001 2002 2003 2004 2005 2006 2007 ... 2013 2014 2015 2016 2017 2018 2019 2020 2021 2022
103 Korea, Dem. People's Rep. PRK 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 ... 0.0 0.0 0.0 0.0 0.0 0.0 NaN NaN NaN NaN

1 rows × 25 columns

Missing values are just a prolongation of nul values, so as there is no information at all I will drop North Korea from the analysis together with the rest of the remaining smaller countries.

Hide code cell source 
# Get indexes of rows with missing values
nan_rows = dfi.index[dfi.isna().sum(axis=1) != 0]

# Drop rows with missing values
dfi = dfi.drop(nan_rows)

# I will keep not interpolated df for plotting with missing values
df = df.drop(nan_rows)

# Get df info
dfi.info()

<class 'pandas.core.frame.DataFrame'>
Index: 205 entries, 0 to 216
Data columns (total 25 columns):
 #   Column        Non-Null Count  Dtype  
---  ------        --------------  -----  
 0   Country Name  205 non-null    object 
 1   Country Code  205 non-null    object 
 2   2000          205 non-null    float64
 3   2001          205 non-null    float64
 4   2002          205 non-null    float64
 5   2003          205 non-null    float64
 6   2004          205 non-null    float64
 7   2005          205 non-null    float64
 8   2006          205 non-null    float64
 9   2007          205 non-null    float64
 10  2008          205 non-null    float64
 11  2009          205 non-null    float64
 12  2010          205 non-null    float64
 13  2011          205 non-null    float64
 14  2012          205 non-null    float64
 15  2013          205 non-null    float64
 16  2014          205 non-null    float64
 17  2015          205 non-null    float64
 18  2016          205 non-null    float64
 19  2017          205 non-null    float64
 20  2018          205 non-null    float64
 21  2019          205 non-null    float64
 22  2020          205 non-null    float64
 23  2021          205 non-null    float64
 24  2022          205 non-null    float64
dtypes: float64(23), object(2)
memory usage: 41.6+ KB

Cluster analysis#

To identify any patterns in the evolution of internet usage across countries, I will proceed to cluster them into different groups using the k-means clustering algorithm.

Hide code cell source 
# Subset samples from dataframe
samples = dfi.loc[:, dfi.columns[2:]]

# Search for number of clusters
inertias = []
clusters = []
for n_clusters in range(1, 10):
    model = KMeans(n_clusters=n_clusters)
    model.fit(samples)
    inertias.append(model.inertia_)
    clusters.append(n_clusters)

# Plot
inertias_df = pd.DataFrame({"n_clusters": clusters, "inertia": inertias})
fig, ax = plt.subplots(figsize=(4, 3))
sns.pointplot(x="n_clusters", y="inertia", data=inertias_df, ax=ax)
sns.despine()
plt.show()
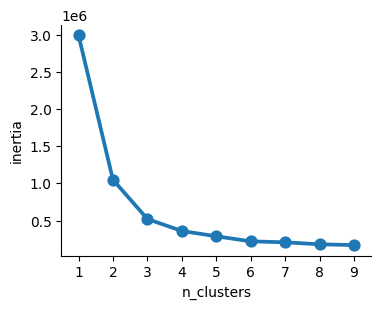
../_images/f181f0d6829ff2f36922ec2be9407a5ca3e37ce94bb94dfbdb104c07d4584510.png

According to the Elbow Method, I choose “3” as the optimal number of clusters.

Therefore, samples will be labeled as either ‘0’, ‘1’, or ‘2’. Once labeled, I will plot the mean values for each group.

Hide code cell source 
# Instantiate model with defined n_clusters
model = KMeans(n_clusters=3, random_state=42)

# Fit the model
model.fit(samples)

# Predict labels
labels = model.predict(samples)

# Insert labels in a new column the dataframe
dfi["label"] = labels
df["label"] = labels

# Subset by cluster label and calculate average values per year
df_0_avg = (
    dfi.loc[dfi["label"] == 0, dfi.select_dtypes(include="float").columns].mean()
).to_frame(name="Cluster 0")
df_1_avg = (
    dfi.loc[dfi["label"] == 1, dfi.select_dtypes(include="float").columns].mean()
).to_frame(name="Cluster 1")
df_2_avg = (
    dfi.loc[dfi["label"] == 2, dfi.select_dtypes(include="float").columns].mean()
).to_frame(name="Cluster 2")

# Join in a single dataframe
df_clusters = df_0_avg.join(df_1_avg).join(df_2_avg).reset_index(names="Year")

# Transform dataframe from wide to long format for plotting
df_clusters_l = df_clusters.melt(
    id_vars="Year", var_name="Cluster", value_name="Internet Usage"
)

# Plot
fig, ax = plt.subplots(figsize=(6, 4))
sns.lineplot(
    ax=ax,
    x="Year",
    y="Internet Usage",
    data=df_clusters_l,
    hue="Cluster",
    errorbar=None,
)
ax.tick_params(axis="x", labelsize=10, rotation=90)
ax.grid(axis="y")
ax.set_axisbelow(True)
ax.set_xlabel("", fontsize=11)
ax.set_ylabel("Internet Usage %", fontsize=12)
ax.set_ylim(0, 100)
sns.despine()
plt.show()
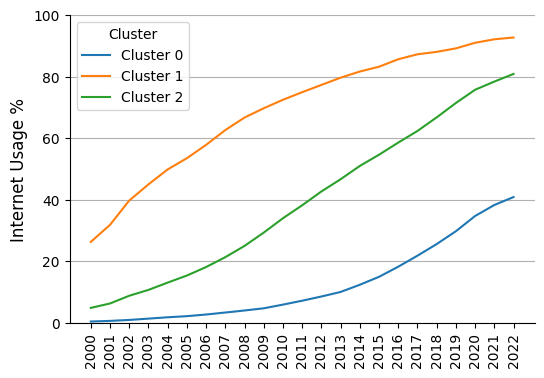
../_images/882a8f485c18f8a5e8b95062011d9c8243ab571b638616de815af67674c5152e.png

The graph shows that the clusters identified by the algorithm correspond to groups of countries with different internet adoption rates and patterns:

  • Cluster 0 -> I name it “late adopters”

  • Cluster 1 -> I name it “early adopters”

  • Cluster 2 -> I name it “mid adopters”

Now that we have identified the clusters, I will replace the labels for clusters ‘0’, ‘1’, and ‘2’ with their corresponding meaningful category names and plot the results using interactive graphs, allowing users to select countries to display alongside the group trends.

Hide code cell source 
# Define categories
categories = ["early", "mid", "late"]

# Replace label number with category name
dfi["label"] = dfi["label"].replace(
    {0: categories[2], 1: categories[0], 2: categories[1]}
)
df["label"] = df["label"].replace(
    {0: categories[2], 1: categories[0], 2: categories[1]}
)

# Replace cluster label with category name
df_clusters_l["Cluster"] = df_clusters_l["Cluster"].replace(
    {"Cluster 0": categories[2], "Cluster 1": categories[0], "Cluster 2": categories[1]}
)
# Rename column name
dfi = dfi.rename(columns={"label": "Adopter"})
df = df.rename(columns={"label": "Adopter"})
df_clusters_l = df_clusters_l.rename(columns={"Cluster": "Adopter"})

# Convert the column to ordered categorical
dfi["Adopter"] = dfi["Adopter"].astype(
    pd.CategoricalDtype(categories=categories, ordered=True)
)
df["Adopter"] = df["Adopter"].astype(
    pd.CategoricalDtype(categories=categories, ordered=True)
)
df_clusters_l["Adopter"] = df_clusters_l["Adopter"].astype(
    pd.CategoricalDtype(categories=categories, ordered=True)
)

# Convert dataframes from wide to long format for plotting
dfi_long = dfi.melt(
    id_vars=["Country Name", "Country Code", "Adopter"],
    var_name="Year",
    value_name="Internet Usage",
)
df_long = df.melt(
    id_vars=["Country Name", "Country Code", "Adopter"],
    var_name="Year",
    value_name="Internet Usage",
)

# Define colors to match the ones that appeared in the clusters plotting
sns_tab10_blue = sns.color_palette("tab10").as_hex()[0]
sns_tab10_orange = sns.color_palette("tab10").as_hex()[1]
sns_tab10_green = sns.color_palette("tab10").as_hex()[2]

# Instance of plotly graphic object
fig = go.Figure()

# Add traces for each adopter type (cluster)
color_key = {"early": sns_tab10_orange, "mid": sns_tab10_green, "late": sns_tab10_blue}
for adopter in categories:  # ["early", "mid", "late"]:
    df_adopter = df_clusters_l.loc[df_clusters_l["Adopter"] == adopter, :]
    fig.add_trace(
        go.Scatter(
            x=df_adopter["Year"],
            y=df_adopter["Internet Usage"],
            mode="lines",
            name=f"{adopter} adopters",
            line=dict(color=color_key[adopter], dash="dot"),
            hovertemplate="%{fullData.name}<br> %{x:.0f}: %{y:.0f}%<extra></extra>",
        )
    )


# Add traces for each country
for country, adopter in zip(dfi["Country Name"], dfi["Adopter"]):
    df_country = df_long.loc[df_long["Country Name"] == country, :]
    fig.add_trace(
        go.Scatter(
            x=df_country["Year"],
            y=df_country["Internet Usage"],
            mode="lines",
            name=country,
            visible="legendonly",  # Hidden when first shown
            line=dict(color=color_key[adopter]),
            hovertemplate="%{fullData.name}<br> %{x:.0f}: %{y:.0f}%<extra></extra>",
        )
    )

# Layout parameters
fig.update_layout(
    # # Set width and height (in pixels)
    # width=1200,
    # height=600,
    # Set the range for the y-axis
    yaxis=dict(range=[0, 100]),
    # Set titles
    title="Internet Usage in the World",
    yaxis_title="% of the population",
)

fig.show()

# Plot world map choropleth
# Read into a geopandas dataframe countries' map and data
# Data downloaded from https://www.naturalearthdata.com/downloads/110m-cultural-vectors/
gdf = gpd.read_file("map/ne_110m_admin_0_countries.shp")

# Select some columns of interest
gdf = gdf.loc[:, ["NAME", "GU_A3", "CONTINENT", "POP_EST", "ECONOMY", "geometry"]]

# Change South Sudan's code to the one used in the dataset, otherwise will not merge and appear in map
gdf.loc[gdf["NAME"] == "S. Sudan", "GU_A3"] = "SSD"

# Merge to the left on geopandas dataframe
gdf_labels = gdf.merge(
    dfi.loc[:, ["Country Name", "Country Code", "Adopter"]],
    how="left",
    left_on="GU_A3",
    right_on="Country Code",
)

# Drop missing values (not matched after merging)
gdf_labels = gdf_labels.dropna()

# Create "id" column for plotting
gdf_labels["id"] = gdf_labels.index.astype(str)

# Wolrd map choropleth
fig = px.choropleth(
    gdf_labels,
    geojson=gdf_labels.__geo_interface__,
    locations="id",
    color="Adopter",
    hover_name="NAME",
    projection="natural earth",
    color_discrete_map={
        "early": sns_tab10_orange,
        "mid": sns_tab10_green,
        "late": sns_tab10_blue,
    },
    category_orders={  # Ensure the legend shows the ordered categories
        "Adopter": ["early", "mid", "late"]
    },
    hover_data={
        "id": False,  # Exclude the 'id' from hover
        "Adopter": True,  # Include 'name' (country names)
    },
)

# fig.update_layout(
#     width=800,
#     height=600,
# )

fig # Apparently, "fig.show()" does not render in jupyter-book!

Conclusions#

The most important conclusion of this study is likely the observation that the rate of growth in internet adoption is slowing down. While in early-adopter and even mid-adopter countries this seems to be due to natural saturation, the slowdown is particularly striking in late-adopter countries, as the proportion of the population using the internet in these countries is still considerably low. This could serve as a warning, indicating the need to invest in infrastructure and resources in these nations.